Come anticipato mostro come ricavare la funzione generatrice dei polinomi di Legendre in un ulteriore modo. Abbiamo visto che la derivata n-esima di tale funzione fornisce l'n-esimo polinomio di Legendre. Allora indichiamola con G(x,t) e calcoliamo lo sviluppo:
)
usando per i polinomi di Legendre la rappresentazione integrale di Laplace seguente:
=\frac{1}{2\pi}\int_{-\pi}^{+\pi}(x+\sqrt{x^2-1}\cos\varphi)^nd\varphi)
Allora si ha:
=\frac{1}{2\pi}\sum_{n=0}^{+\infty}t^n\int_{-\pi}^{+\pi}(x+\sqrt{x^2-1}\cos\varphi)^nd\varphi=)
\]^n\}d\varphi=)
}d\varphi=\frac{1}{\sqrt{1-2xt+t^2}})
ammesso che t sia limitato ai valori tali che:
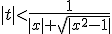
cosa che assicura la possibilità di scambiare somma e integrale come conseguenza della convergenza uniforme della serie geometrica.
L'integrale nell'ultimo passaggio si risolve con tecniche di integrazione complessa. Puoi vedere la dimostrazione cliccando qui.
[Chiudi]Consideriamo l'integrale:
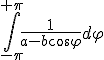
di cui quello considerato sopra rappresenta un caso particolare con a = 1 - tx e b = t√x
2-1 e che possiamo riscrivere, con alcune semplici manipolazioni algebriche, come:
}}\frac{dz}{bz^2-2az+b})
eseguendo la sostituzione:
)
Si noti come tale sostituzione mandi l'intervallo in φ da -π a +π nella circonferenza di raggio unitario centrata nell'origine (in z). Ora si usa il teorema dei residui:
}}f(z)dz=2\pi i\sum_{k}Res\quad f(z)|_{z=z_k})
dove con z
k abbiamo indicato i poli della funzione f(z) all'interno della curva C
1(0). I poli della funzione integranda in questione sono:
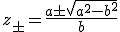
di cui solo z
- interno a C
1(0) se |b|<|a|, come è in questo caso e si può mostrare usando la disuguaglianza |A-B|>|A|-|B| e la relazione che limita i possibili valori di t. Infatti:
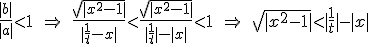
da cui:
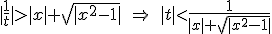
relazione questa che abbiamo detto essere soddisfatta per garantire l'interscambiabilità tra somma ed integrale. Immediatamente allora si trova:
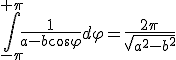
relazione che scritta in termini di x e t da il risultato voluto.








0 commenti:
Posta un commento